Abstract
This paper investigates the spectral efficiency (SE) optimization in muti-group (MG) multicast (MC) multiple-input multiple-output (MIMO) cognitive radio (CR) systems with the assistance of an active intelligent reflecting surface (IRS). The research aims at designing the transmit precoders (TPCs) at the secondary base station (SBS) and the reflection coefficients (RCs) at the IRS to maximize either the sum rates of MC groups or the minimum rates among MC groups in the secondary network while guaranteeing transmit power (TP) budget constraints at the SBS and reflection amplitude and amplification power at the IRS, and the interference power (IP) constraints at the primary users (PUs). To address the challenges of coupled variables in the formulated design problems, we exploit the alternating optimization (AO) to decompose the design problems into amenable sub-problems. To tackle the difficulties posed by the nonconvex nature of the design problems, we derive the surrogate functions to transform the optimization problems into convex forms. Then, efficient iterative algorithms are derived to obtain the optimal SBS TPCs and IRS RCs. The numerical simulations are conducted to investigate the system performance over the various system parameters. The numerical results demonstrate that maximizing the minimum rates leads to fairer distributions of achievable rates among groups, while maximizing the sum rate offers higher achievable rates for favorable groups. The results also reveal that systems with optimized IRS RCs obtain superior rates compared to those with fixed IRS RCs.
Introduction
To address the growing demands of emerging wireless communication applications, spectral efficiency (SE) and energy efficiency (EE) techniques are crucial considerations in the design of future wireless communication systems (WCSs). Cognitive radio (CR) is recognized as an effective way to utilize the radio spectrum. However, given the ongoing demands for wireless networks with better quality of service features such as higher data rates, low power consumption, greater EE, and improved SE, novel technologies are being investigated for the next generation of WCSs. A recent novel technology stemming from advancements in micro-electro-mechanical systems has introduced intelligent reflecting surfaces (IRSs) with low-cost and energy-effective characteristics. These surfaces can be dynamically reconfigured to create intelligent wireless propagation environments 1 , 2 . By intelligently altering the reflection coefficients (RCs), the IRS can adjust the phase shifts of the reflected electromagnetic waves to boost the desired signals and mitigate interference signals. Passive IRSs (pIRSs) have been extensively studied in various WCSs 3 , 4 . The studied results demonstrated the benefits of deploying the IRSs in WCSs in terms of performance gains and effective costs 1 . However, multiplicative fading effects relevant to IRSs limit the achievable gains of pIRSs. Recently, active IRSs (aIRSs), which can amplify incident signals, have developed by integrating reflection-type amplifiers into their structures 5 . Recent works 5 , 6 showed that aIRSs could overcome the negative impacts of multiplicative fading. Due to the advantages of IRSs, the integration of IRSs into various WCSs to further enhance SE and EE has attracted considerable search attention 7 .
IRSs have been studied in CR networks with various scenarios. The authors 8 investigated the pIRS-aided CR network with two pairs of single-antenna primary users (PUs) and secondary users (SUs). The authors optimized the transmit power (TP) at the SUs and the RCs at the IRS to maximize the SU rate. Alternatively, the authors 1 designed the transmit precoders (TPCs) and RCs to minimize mean squared error for multiuser multiple-input multiple-output (MIMO) CR networks with the assistance of an aIRS. Reference [9] studied the aIRS-aided MIMO simultaneous wireless information and power transfer (SWIPT) CR systems in which the SE maximization was studied with the constraints of TP, amplification power, interference power (IP), and harvested energy. Alternatively, reference [10] concerned the EE in the pIRS-aided MIMO SWIPT CR systems.
The majority of aforementioned studies 1 , 8 , 9 , 10 focused on deploying IRSs for unicast transmission in which each user is designed to receive independent data streams. Such unicast transmission can suffer from severe interference and poor performance, especially as the number of users grows 11 . In practice, a group of users may simultaneously request identical messages, such as applications of television programs and video conferences. In such scenarios, multicast (MC) transmission in which the same messages are transmitted to the users in a group is of significant interest 11 .
Different from most of the previous works 1 , 8 , 9 , 10 focusing on unicast scenarios in which distinct data streams are sent to each user, our paper is concerned with the deployment of an aIRS for multi-group (MG) MC scenarios. Concerning MC transmission, reference 12 investigated the optimal beamforming design for MG MC multiple-input single-output (MISO) CR systems in which efficient optimization algorithms were proposed to tackle design problems of the TP minimization and signal-to-interference-plus-noise-ratio (SINR) maximization. More recently, the authors 13 derived the optimal beamforming structures to facilitate the numerical optimization algorithms for the beamforming design problems in MG MC MISO systems. Similarly, the work 14 investigated the MG MC SWIPT MISO system without IRSs. Alternatively, reference 11 considered the MG MC MISO system with the aid of a pIRS. Therein, the transmit beamformers and IRS RCs are optimized to maximize the overall sum rate. Similarly, reference 15 studied the MG MC MISO system with the pIRS. By considering imperfect channel state information (CSI), the transmit beamforming vectors and IRS RCs are designed to optimize the max-min SINR fairness problem. The authors 16 studied the outage probability of the WCS in which the single-antenna base station transmits a common message to multiple single-antenna users with the aid of a pIRS of random phase shifts.
Against this background, in the present paper, we study a MG MC CR system in which a multiple-antenna secondary base station (SBS) sends distinct data streams to MC groups in downlink transmission. The multiple-antenna users in the same MC group receive identical data streams while suffering interference from the data streams of other groups. In addition, in CR networks, the transmission in the secondary network must not cause adverse interference to the PUs. An aIRS is employed to improve the SE in the secondary network and mitigate IP caused at the PUs. Our aim is to optimally design the TPCs at the SBS and RCs at the aIRS to maximize the SE. To the best of our knowledge, the optimal joint design of the SBS TPCs and IRS RCs for SE enhancement in MG MC MIMO CR systems with the application of an aIRS has not been thoroughly investigated. In this work, we aim to maximize either the sum rates of MC groups or minimum rates among MC groups under the constraints of power budgets at the SBS, RC amplitudes and amplification power at the aIRS, and IP at the PUs. The formulated design problems are mathematically intractable to be directly solved due to the high coupling of design variables and the nonconvexity of the optimization problems. Accordingly, to achieve the optimal solutions, we develop efficient iterative algorithms. Specifically, the main contributions of our work can be listed as follows:
Firstly, we introduce the MG MC CR MIMO systems model with the assistance of an aIRS in which the users in a MC group can receive common data streams, and the SUs share the common spectrum with the PUs. To highlight the novelty of this paper, we emphasize that most previous research focuses on either unicast transmission with the deployment of a pIRS or without an IRS, or without CR. In contrast, we investigate a more general scenario of MG MC transmission with the assistance of an aIRS in a MIMO CR network. We aim at the optimal design of the TPCs at the SBS and the RCs at the IRS to maximize either the sum rates of the MC groups or minimum rates among MC groups under the constraints of TP at the SBS, reflection amplitude, and power amplification at the aIRS, and the IP at the PUs. The resultant optimization problems are highly nonconvex and mathematically intricate since the objective functions (OFs) and constraints involve the nonlinearly coupled variables.
Secondly, we develop efficient optimization algorithms by leveraging the combination of alternating optimization (AO) and minorization-maximization (MiMa) frameworks to find the optimal designs. Specifically, our strategy is to alternatively optimize sub-problems in which either the TPCs or RCs are optimized for the other variables fixed. Then, in each sub-problem, by utilizing the MiMa technique, we exploit the concave minorant of the user rate function to alter the sub-problem into a convex one. Thus, the developed iterative algorithms can be guaranteed convergence and have the polynomial-time computational complexity.
Finally, we conduct numerical simulations to demonstrate the achievable SE performance of the considered system and the effectiveness of the proposed algorithm. In addition, we also investigate the impacts of different system parameters on the achievable SE. The simulation results indicate that the minimum rate maximization (MRM) approach provides fairer rates among groups, while the sum rate maximization (SRM) offers higher rates for favorable groups. They also show that the optimized IRS RCs can significantly improve the achievable SE compared to fixed IRS RCs.
The rest of the paper is presented as follows. In Section II, we introduce the system model, and then formulate the design problems. Section III derives iterative algorithms to find the optimal designs of the TPCs and RCs to maximize the SE. Then, the numerical results and discussion are presented in Section IV while the conclusions of the paper are given in Section V.
Notations: For a matrix M, notations M
T
and M
H
represent the transpose and Hermitian of a matrix while
System Model and Problem Formulation
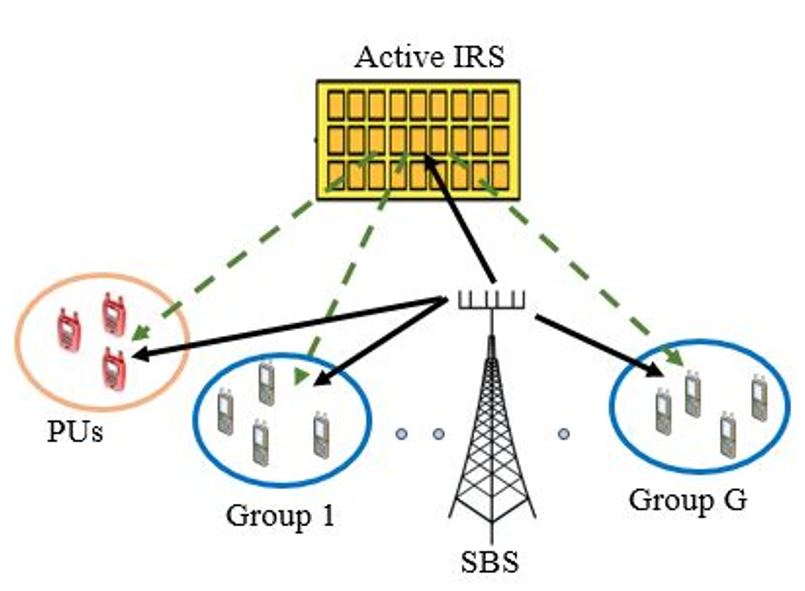
Consider an integration of an aIRS in a MG MC MU-MIMO CR system as shown in Figure 1 . The SBS with N B antennas transmits the data streams to G groups in the downlink channels. Denote G = {1, 2, ..., g} as the set of all groups and K g = {1, 2, ..., K g } as the set of SUs in group g where K g is the number of users in group g. Each SU with N u antennas belongs to a single MC group, resulting in the total number of SUs in the system as . The secondary system operating in the underlay models of CR transmissions utilizes the frequency spectrum allocated to the primary system which comprises P PUs denoted by P = {1, 2, ..., P}. Each PU is equipped with N p antennas. Define the data symbol vector intended to SUs in group g as where d g ≤ min{N B , N u } is the number of data streams of users in group g and E(s g s H g ) = I dg , E(s g s H l ) = 0 for g ≠ l. To mitigate interference and improve transmission performance, the data symbol vector of SU k in group g (denoted as SU k,g ) is linearly processed by the TPCs . Then, the transmitted baseband signal at the SBS is expressed as Eq.1 ( Figure 2 )
To further enhance the secondary network performance and also mitigate interference imposed on the PUs, an aIRS composed of N reflection elements (REs) is deployed. Distinct from pIRSs, aRISs can simultaneously manipulate the phase and amplitude of the incident signals. Denoting the reflection amplitude and phase shift of RE n as a n ∈ [0, a n max ] and θ n ∈ (0, 2π] for n ∈ N = {1,...,N}, the IRS RC matrix is represented by Φ = diag(ϕ 1 , ϕ2 ..., ϕ N ) where ϕ N = a n e jθn is the reflection coefficient of RE n. By adopting the frequency-flat fading channel models, the channel matrix from the SBS to the IRS is denoted as . Then, the aIRS produces the output signal power 1 as Eq. 2 ( Figure 2 )
where σ I 2 is noise power at each RE. The aIRS exploits additional power sources to amplify the incident signals, and thus the amplification power of the aIRS is constrained as 1 Eq. 3 ( Figure 2 )
where P IRS max is the maximum amplification power.
Regarding the received signals at the SUs, denote the channel matrices from the SBS to SU k,g and from the IRS to SU k,g as and , respectively. Accordingly, the received signal at SU k,g is given by Eq.4 ( Figure 2 ).
where is the effective channel from the SBS to SU k,g and from SBS to IRS to SU k,g . Vectors are additive noise at the IRS and SU k,g , respectively 7 . In equation (4), the first term is the desired signal at SU k,g while the second term is interference between the MC groups, the third term is additive noise from the aIRS, and the last term is additive noise at the receiver. Therefore, the achievable rate (nats/s/Hz) of SU k,g is Eq. 5 ( Figure 2 ).
where we have denoted and . In MG MC transmissions, the users in a group decode the identical data streams. Thus, the achievable rates of MC group g is given by 11 Eq. 6 ( Figure 2 ).
Concerning the PUs, we denote and as the channels from the SBS to PU p and from the IRS to PU p respectively. Then, the total IP at PU p is computed by Eq. 7 ( Figure 2 ).
where H p = H d,p + H r,p + ΦG. For underlay CR models, to guarantee the performance of the PUs, the CR system cannot cause the total IP at each PU to be greater than a tolerance threshold. Thus, the IP constraints are expressed as 1 Eq. 8 ( Figure 2 ).
where γ p is an acceptable IP threshold at PU p .
To investigate the achievable system performance, the quasi-static flat-fading channel models are adopted, and perfect CSI is available at the SBS 2 . Then, our target is to jointly design the TPCs W and RCs Φ to maximize either the sum rates of the MC groups or the minimum rate fairness of the MC groups subject to the constraints of the SBS TP budget, the amplification power at the aIRS, the reflection amplitude of REs, the IP restrictions imposed on the PUs.
A. Maximization of the sum rates of MC groups
In communication systems, maximizing the total SE is of practical importance. Thus, the SRM of MC groups is formulated as the following optimization problem: Eq. 9 ( Figure 2 ).
where represents the TP budget allocated to the SBS.
B. Maximization of the minimum rate among MC groups
The SRM problems of the MC groups generally result in unfairness among groups. Thus, to improve the fairness among MC groups, we maximize the minimum achievable rate among MC groups, which is expressed as the MRM: Eq. 10 ( Figure 2 )
Notice that problems (9) and (10) are highly intractable due to the non-concave nature of the OFs, non-convexity of the constraints, and intricate couplings of the design variables. Next section is devoted to developing iterative algorithms to obtain optimal solutions to these non-convex problems.
PROPOSED METHOD FOR SE OPTIMIZATION
This section will develop iterative optimization algorithms to solve SRM problem (9) and MRM problem (10). First, we focus on solving SRM problem , and then extend the approach for MRM problem (10).
A. Proposed method for the SRM of MC groups
First, problem (9) is equivalently rewritten as Eq. 11 ( Figure 2 )
The above optimization problem is difficult to solve directly due to intricately coupled optimization variables. Thus, by capitalizing on the AO framework, we decompose the original optimization problem in (11) into two subproblems.
A. Proposed method for the SRM of MC groups
First, problem (9) is equivalently rewritten as Eq. 11 ( Figure 2 )
The above optimization problem is difficult to solve directly due to intricately coupled optimization variables. Thus, by capitalizing on the AO framework, we decompose the original optimization problem in (11) into two subproblems.
A. Proposed method for the SRM of MC groups
First, problem (9) is equivalently rewritten as Eq. 11 ( Figure 2 )
The above optimization problem is difficult to solve directly due to intricately coupled optimization variables. Thus, by capitalizing on the AO framework, we decompose the original optimization problem in (11) into two subproblems.
A. Proposed method for the SRM of MC groups
First, problem (9) is equivalently rewritten as Eq. 11 ( Figure 2 )
The above optimization problem is difficult to solve directly due to intricately coupled optimization variables. Thus, by capitalizing on the AO framework, we decompose the original optimization problem in (11) into two subproblems.
B. Proposed method for the maximization of the minimum rate among MC groups
Similar to the derivations in subsection III-A, problem (10) is reformulated as Eq. (20)
B. Proposed method for the maximization of the minimum rate among MC groups
Similar to the derivations in subsection III-A, problem (10) is reformulated as Eq. (20)
B. Proposed method for the maximization of the minimum rate among MC groups
Similar to the derivations in subsection III-A, problem (10) is reformulated as Eq. (20)
B. Proposed method for the maximization of the minimum rate among MC groups
Similar to the derivations in subsection III-A, problem (10) is reformulated as Eq. (20)
C. Convergence and computational complexity
Note that the iterative procedures in solving subproblems 1 and 2 for seeking the optimal TPCs and RCs are provable convergence according to the principles of MiMa methods 20 . In addition, the AO approaches in Algorithms 1 and 2 guarantee that their corresponding OFs are nondecreasing over iterations. Furthermore, the OFs are upper bounded for the feasible sets of the considered constraints. Thus, the convergence properties of Algorithms 1 and 2 are guaranteed.
Regarding the computational complexity, Algorithms 1 and 2 rely on convex optimization, and thus, the proposed optimization algorithms exhibit a polynomial time computational complexity.
SIMULATION RESULTS AND DISCUSSION
This section presents numerical investigations on the achievable SE performance of the proposed optimization algorithms for aIRS-aided MG MC CR systems with various system settings. In numerical simulations, the system consists of one SBS with N B = 4 antennas, one aIRS, G = 2 groups, K g = 3 SUs in each group, and P = 2 PUs. Each user is equipped with N u = N p = 2 antennas and each MC group is expected to receive d g = 2 data streams. The SBS is at position (0, 0) m while the IRS is at position (0, 30) m. The SUs in group g are randomly located in a circle with a radius 10 m 1 . The center of group 1 is at position (100, 0) and that of group 2 is at position (-100, 0). The PUs are randomly distributed in a circle with the center at (-200, 0) m and a radius of 10 m 9 . The channel coefficients for the transmission distance d rt between transmitter t and receiver r are modelled by Eq. 23 ( Figure 2 ).
Here, L r,t = L 0 (d rt /d 0 ) -αrt is the path loss where L 0 = 10 -3 is the pathloss at the reference distance d 0 = 1 m and α rt is the path loss exponent 21 . Small scale fading channels , respectively are deterministic line-of-sight (LoS) and Rayleigh fading non-LoS (NLoS) components of channels with the Rician factor κ rt . IRS-related channels are modeled as the Rician fading channels with the Rician factor of 3 and the path loss exponents of 2.2 while other channels are modeled as the Rayleigh fading channels with the path loss exponents of 3.6. The noise powers at the SUs and the IRS are σ 2 k,g = σ I 2 = -100 dBm. The allowable IP at the PU is set as γ p = -100 dBm. Regarding the iterative algorithms, we set = 10 -3 , T max = 100. Unless specified, the other parameters are given as follows. The TP budget at the SBS is = 10 dBm. The number of active REs is N = 20. The maximum reflection amplitude coefficients are = a max = 1.9 and maximum amplification power at the IRS is = 10 dBm. The simulations are conducted over 100 random channel realizations to compute the average numerical results.
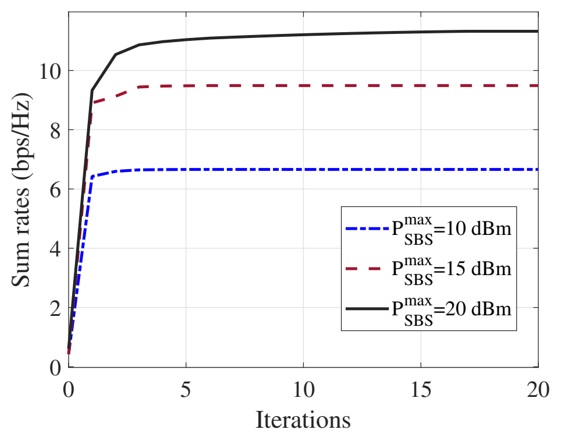
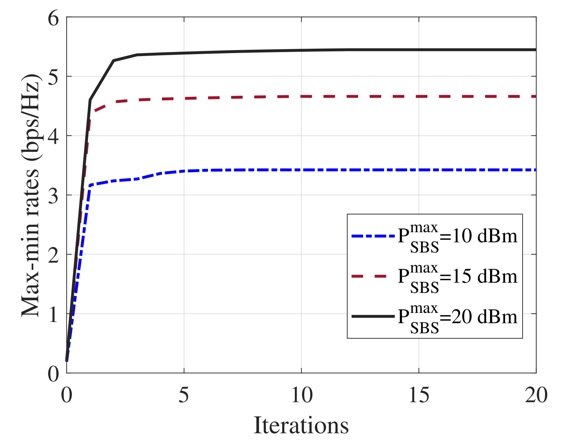
Example 1 : First, we investigate the convergence characteristics of the proposed AO algorithms for the SRM and MRM of MC groups. To this end, we visualize the OF values obtained over iterations in Figure 5 and Figure 6 for a random channel realization with different SBS TP budgets. The results in these figures show the non-decreasing characteristics of the OF values versus iterations, which verifies the convergence of the proposed AO algorithms. In addition, the OF values converge to stable points within less than 20 iterations. On the other hand, as expected, the higher OF values are obtained when the TP budgets at the SBS grow.
Figure 5 . The OF values over iterations of the proposed AO algorithm for the SRM of MC groups.
Figure 6 . The OF values over iterations of the proposed AO algorithm for the MRM of MC groups.
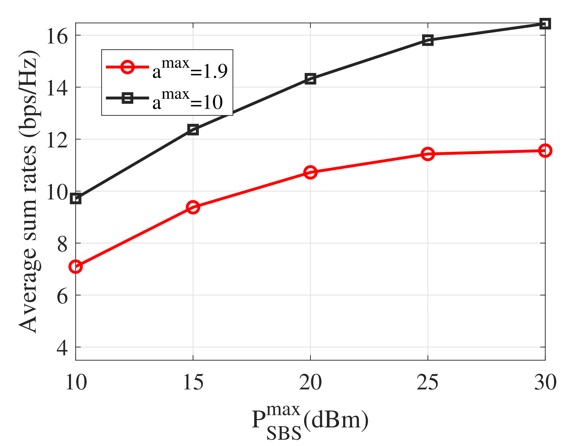
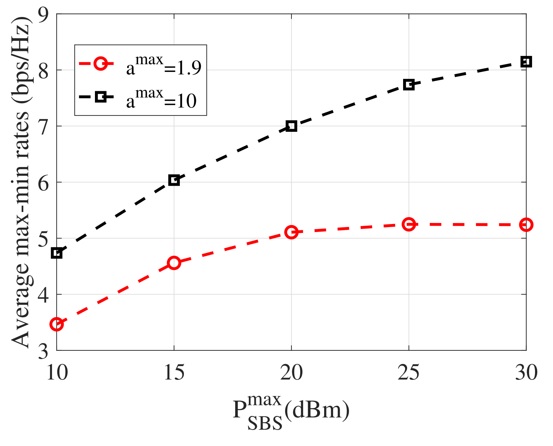
Example 2: Next, to study more insights into the effects of the SBS TP budgets on the achievable SE of the considered system, we visualize the average achievable sum rates and max-min rates versus the SBS TP budgets in Figure 7 and Figure 8 respectively for different values of maximum reflection amplitude coefficients. From these figures, we can observe that the achievable rates increase with the SBS TP budget. However, when maximum reflection amplitudes at the IRS are low (e.g., a max = 1.9), the achievable rates become saturated as the SBS TP budget is large. This provides useful insights in selecting the appropriate SBS TP budgets and maximum reflection amplitudes of the active IRS to obtain the desired rates. Specifically, from Figure 7 and Figure 8 for the IRS with the maximum reflection amplitudes a max = 1.9, an increase in the SBS TP budgets from 25 dBm to 30 dBm is not useful since the SE improvements are negligible. This phenomenon can be explained as follows: When the SBS TP budget is low, the IP constraints at the PUs and reflection amplification power and amplitude constraints at the aIRS are inactive. Thus, the SBS can exploit the maximum TP to increase the achievable rates. However, when the SBS TP budget is sufficiently large, the design problems are restricted by IP constraints and/or reflection amplification power and amplitude constraints, preventing the SBS from utilizing the full TP budget. Consequently, the achievable rates cannot increase further.
Figure 8 . Average achievable max-min rates among MC groups versus the SBS TP budgets.
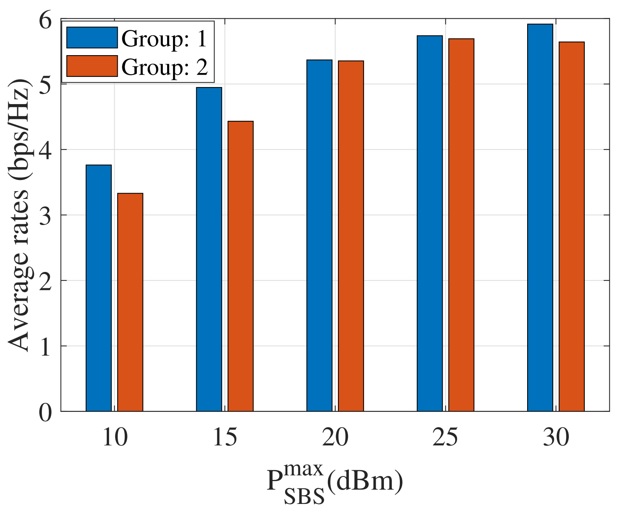
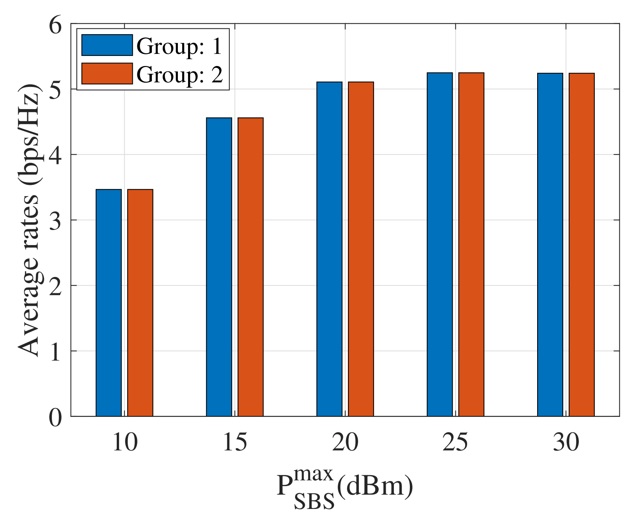
To further investigate the fairness in terms of achievable rates of groups, we visualize the average achievable rates of MC groups obtained by the SRM in Figure 9 , and those obtained by the MRM in Fig. Obviously, from Figure 9 , the MC group 1 achieves higher rates than the MC group 2. That is because MC group 2 in the simulation setting is located close to the PUs, and the SBS and IRS steer the signals away from the PUs to mitigate interference. In contrast, by applying the MRM, MC groups achieve the same average rates as demonstrated in Figure 10 , which provides fairness among groups.
Figure 9 . Average achievable rates of MC groups versus the SBS TP budgets by using the SRM algorithm.
Figure 10 . Average achievable rates among MC groups versus the SBS TP budgets by using the MRM algorithm.
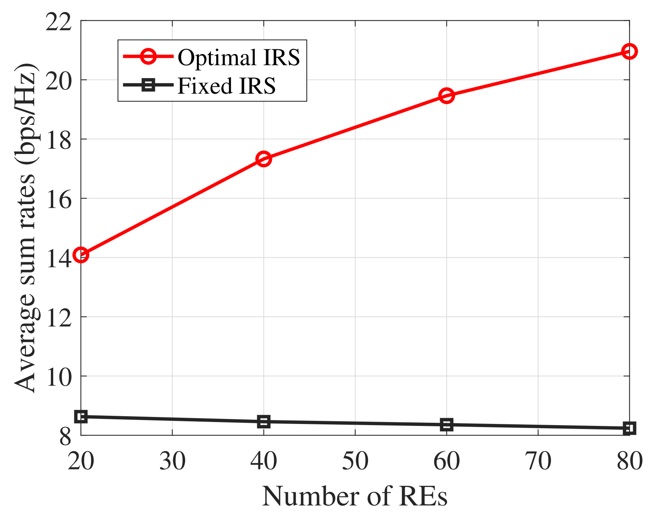
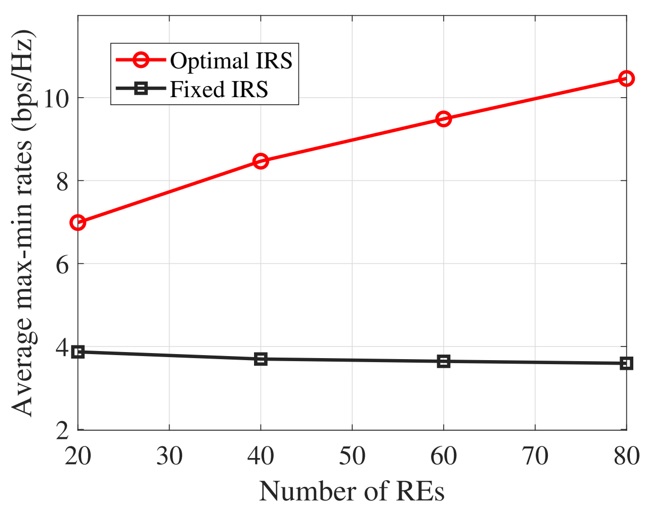
Example 3 : Finally, we study the impacts of the number of IRS REs on the achievable SE performance. In addition, to validate the effectiveness of our proposed optimization algorithms, a baseline scheme, namely, fixed IRS, in which the reflection coefficients at the IRS are fixed (i.e., Φ = a max I N ) while the TPCs are optimally designed. Figure 8 and Figure 9 visualize the achievable sum rates of MC groups and the minimum rates of MC groups versus the number of IRS REs with the maximum reflection amplitude a max = 10. From these figures, the achievable SE curves for optimized designs by the proposed AO algorithms offer upward trends with the number of IRS Res, while those of fixed IRSs are decreased with the number of IRS REs. These numerical results reveal that the deployment of the active IRS with a greater number of REs can improve the SE if the RCs are optimally designed; otherwise, the SE can degrade if the IRS RCs are fixed.
Figure 11 . Average achievable rates of MC groups versus the number of IRS REs by using the SRM algorithm.
Figure 12 . Average achievable max-min rates among MC groups versus the number of IRS REs by using the MRM algorithm.
Conclusion
We have investigated the SE of MG MC MIMO CR systems with the deployment of an aIRS. Concerning the SE, we formulate two optimization design problems, namely the SRM and the MRM. To tackle the nonconvex formulated design problems, we develop efficient iterative algorithms capitalizing on the AO frameworks with the utilization of the MiMa principle, which renders solving convex optimization problems in iterations. The simulation results have demonstrated the fast convergence of the proposed optimization algorithms. The numerical results have offered valuable insights into the SE performance of the aIRS-aided MC MG CR MIMO systems under the different SBS TP budgets, IRS reflection amplitude coefficients, number of IRS REs. The results have also verified the superior performance in terms of the SE of the systems with the optimally designed IRS RCs in comparison with the systems with fixed IRS RCs.
acknowledgments
This research is funded by Vietnam National University HoChiMinh City (VNU-HCM) under grant number: B2023-20-09 . We acknowledge Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for supporting this study.
CONFLICTS OF INTERESTS
The authors declare no competing interests associated with the publication of this article.
AUTHORS’ CONTRIBUTION
Ha Hoang Kha: Conceptualization, Methodology, Investigation, Writing - Original Draft, Funding acquisition. Xuan-Xinh Nguyen, Kiet Tuan Vo: Software, Writing - Review & Editing. Dinh Quoc Hung: Software and Editing. All authors have read and approved the final manuscript.
References
- Allu R.. Robust beamformer design in active RIS-assisted multiuser MIMO cognitive radio networks. IEEE Trans. on Cogn. Commun. Netw., vol. 9, no. 2, pp. 398–413, April 2023. . ;:. Google Scholar
- Jiang W.. Joint transmit precoding and reflect beamforming design for IRS-assisted MIMO cognitive radio systems,” IEEE Trans. Wireless Commun., vol. 21, no. 6, pp. 3617–3631, 2022. . ;:. Google Scholar
- Wu Q., Zhang R.. Weighted sum power maximization for intelligent reflecting surface aided SWIPT,” IEEE Wireless Commun. Lett., vol. 9, no. 5, pp. 586–590, 2020. . ;:. Google Scholar
- Quyet P. V., Kha H. H.. Energy harvesting maximization for multiuser MIMO SWIPT systems with intelligent reflecting surfaces. Telecommun. Syst., no. 80, pp. 497–511, 2022. . ;:. Google Scholar
- Zhang Z.. Active RIS vs. passive RIS: Which will prevail in 6G? IEEE Trans. Commun., vol. 71, no. 3, pp. 1707–1725, 2023. . ;:. Google Scholar
- Zhi K.. Active RIS versus passive RIS: Which is superior with the same power budget? IEEE Commun. Lett., vol. 26, no. 5, pp. 1150–1154, 2022. . ;:. Google Scholar
- Gao Y.. Beamforming optimization for active intelligent reflecting surface-aided SWIPT. IEEE Trans. Wireless Commun., vol. 22, no. 1, pp. 362–378, Jan 2023. . ;:. Google Scholar
- Guan X.. Joint power control and passive beamforming in IRS-assisted spectrum sharing. IEEE Commun. Lett., vol. 24, no. 7, pp. 1553–1557, 2020. . ;:. Google Scholar
- Quyet P. V., Kha H. H.. Robust transmission design for active IRS aided multiuser MIMO cognitive radio systems with non-linear energy harvesting models. Telecommun. Syst., pp. 1–17, Mar. 2024. . ;:. Google Scholar
- Quyet P. Van, Kha H. H.. Energy efficiency optimization for IRS aided multiuser MIMO SWIPT cognitive radio systems with imperfect CSI. in 2023 Int. Symp. Electrical and Electronics Engr. (ISEE), 2023, pp. 85–90. . ;:. Google Scholar
- Zhou G.. Intelligent reflecting surface aided multigroup multicast MISO communication systems. IEEE Trans. Signal Process., vol. 68, pp. 3236–3251, 2020. . ;:. Google Scholar
- Phan A. H.. Nonsmooth optimization for efficient beamforming in cognitive radio multicast transmission. IEEE Trans. Signal Process., vol. 60, no. 6, pp. 2941– 2951, 2012. . ;:. Google Scholar
- Dong M., Wang Q.. Multi-group multicast beamforming: Optimal structure and efficient algorithms. IEEE Trans. Signal Process., vol. 68, pp. 3738–3753, 2020. . ;:. Google Scholar
- Gautam S.. Weighted sum-SINR and fairness optimization for SWIPT-multigroup multicasting systems with heterogeneous users. IEEE Open J. of the Commun. Society, vol. 1, pp. 1470–1484, 2020. . ;:. Google Scholar
- Jiang W.. Robust design of IRS-aided multi-group multicast system with imperfect CSI. IEEE Trans. Wireless Commun., vol. 22, no. 9, pp. 6314–6328, 2023. . ;:. Google Scholar
- Tao Q.. Intelligent reflecting surface aided multicasting with random passive beamforming. IEEE Wireless Commun. Lett., vol. 10, no. 1, pp. 92–96, 2021. . ;:. Google Scholar
- Tam H. H. M.. Successive convex quadratic programming for quality-of-service management in full-duplex MU-MIMO multicell networks. IEEE Trans. Commun., vol. 64, no. 6, pp. 2340–2353, Jun. 2016. . ;:. Google Scholar
- Tam H. H. M.. MIMO energy harvesting in full-duplex multi-user networks. IEEE Trans. Wireless Commun., vol. 16, no. 5, pp. 3282–3297, 2017. . ;:. Google Scholar
- Grant M., Boyd CVX: MATLAB software for disciplined convex programming. 2020. . ;:. Google Scholar
- Sun Y.. Majorization-minimization algorithms in signal processing, communications, and machine learning. IEEE Trans. Signal Process., vol. 65, no. 3, pp. 794–816, 2017. . ;:. Google Scholar
- Pan C.. Intelligent reflecting surface aided MIMO broadcasting for simultaneous wireless information and power transfer. IEEE J. Sel. Areas Commun., vol. 38, no. 8, pp. 1719–1734, 2020. . ;:. Google Scholar

 Open Access
Open Access