Abstract
The effectiveness of ammunition depends on many factors, of which the miss distance of artillery shells when using the radio proximity fuse utilizing the Doppler is one of the very important parameters when researching, designing, manufacturing fuses and directly affects the effect of artillery shells. Determining this parameter allows the selection of other technical parameters in the radio proximity fuse. This issue has always received the attention of many scientists, but so far, no specific research has been published. This paper presents the theoretical basis to determine the miss distance of artillery shells when using the radio proximity fuse utilizing the Doppler using analytical methods. Based on the target detection area and the fragment area, the article has shown the relationship between the miss distance of artillery shells, the warhead operating angle, and the phase of the miss distance. On that basis, the author has evaluated the change in the value of the miss distance of artillery shells when changing the warhead operating angle, the phase of the miss distance using Matlab software. The results have shown that the value of the miss distance of artillery shells depends significantly on the warhead operating angle, the phase of the miss distance, and the distance between the antenna position and the detonation position of the warhead. The results obtained can be applied to calculate and design the radio proximity fuse utilizing the Doppler effect for artillery shells to destroy aircrafts.
Đặt vấn đề
Đã có nhiều công trình nghiên cứu về sự phối hợp tối ưu giữa luồng mảnh văng và cánh sóng ăng-ten của ngòi nổ 1 , 2 , 3 , 4 , 5 , 6 , 7 . Công trình mô phỏng ngòi nổ cho tên lửa phòng không tầm thấp 2 bàn về khả năng chống nhiễu và dẫn đường của hệ thống ra-đa gần. Hiệu ứng Doppler đã được tác giả S. Veksin sử dụng trong ngòi nổ cận đích 3 . Tại Việt Nam, giá trị trượt mục tiêu có được đề cập sơ lược và chưa có đánh giá cụ thể 8 .
Đạn sát thương bằng mảnh tiêu diệt hoặc sát thương mục tiêu bằng mảnh văng ở khoảng cách nhất định. Nó được gọi là giá trị trượt mục tiêu của đạn. Khi giá trị của nó từ vài mét đến vài chục mét thì hệ thống xác định vị trí đạn và mục tiêu đặt ở đài quan sát bên ngoài đạn coi 2 vị trí này trùng nhau. Điều này gây khó khăn để xác định được giá trị trượt mục tiêu của đạn. Phương pháp giải tích và phần mềm Matlab được sử dụng tính toán việc thiết lập mối quan hệ giữa giá trị trượt mục tiêu, góc kích nổ đạn, pha của độ trượt, khoảng cách giữa vị trí ăng-ten và vị trí kích nổ của đầu đạn giúp cho người thiết kế ngòi đạn có đánh giá khách quan và tương đối tường minh khi lựa chọn các thông số kết cấu.
Phương pháp
Hệ tọa độ
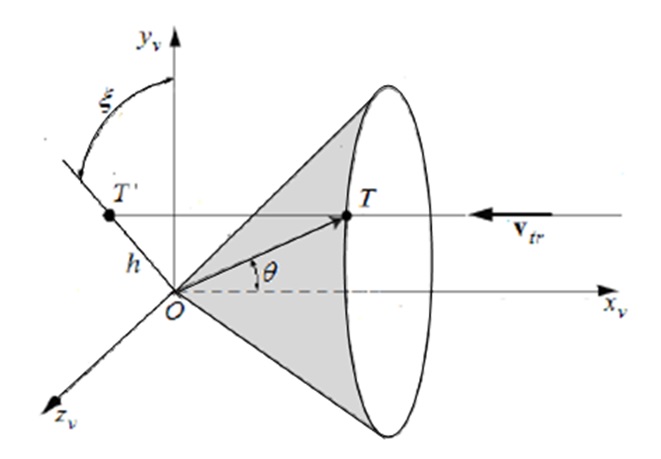
Để xác định tần số Doppler người ta sử dụng hệ tọa độ hình nón liên kết với hệ tọa độ vận tốc thẳng 𝑂𝑥 𝑣 𝑦 𝑣 𝑧 𝑣 , với gốc tọa độ đặt tại vị trí ăng-ten phát của hệ thống ra-đa ( Figure 1 ). Trong đó trục 𝑂𝑥 𝑣 Oy 𝑣 song song với véc-tơ vận tốc tương đối đạn - mục tiêu 𝑣 𝑟𝑡 , mặt phẳng tọa độ 𝑂𝑥 𝑣 𝑦 𝑣 trùng với mặt phẳng tam giác vận tốc được tạo thành từ các véc-tơ vận tốc: v r , v t , v rt . Trong đó, v r ;v t lần lượt tương ứng là vận tốc đạn và vận tốc mục tiêu. Vị trí của mục tiêu tại điểm T và được xác định bởi các đại lượng: x v , h, ξ, trong đóx v là tọa độ Đề-các; h là khoảng cách từ gốc tọa độ O đến hình chiếu T ′ của điểm T trên mặt phẳng Oy v z v , đặc trưng cho độ chính xác dẫn và được gọi là độ trượt; góc cực ξ là pha của độ trượt. h, ξ là tọa độ cực của điểm T ′ .
Trên Figure 1 thể hiện vị trí tương đối của đạn và mục tiêu trong không gian, với vị trí của đạn tại O và vị trí mục tiêu tại T.
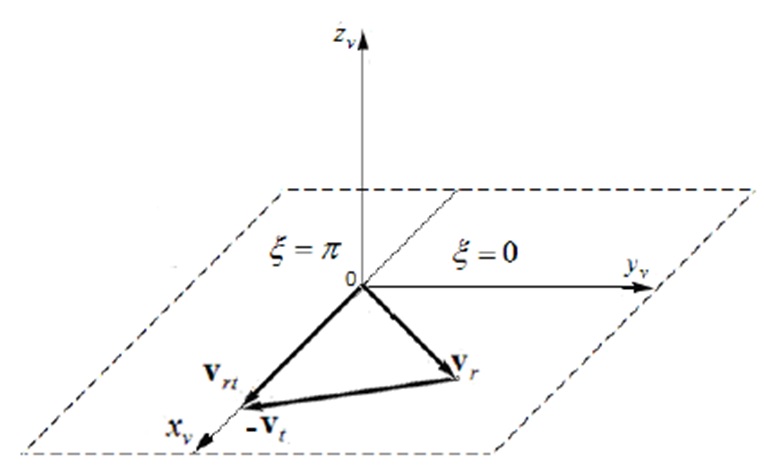
Từ hệ tọa độ dùng để xác định vùng kích nổ đạn ( Figure 1 , Figure 2 ) có thể đưa ra 2 nhận xét sau:
- Nếu độ trượt h = const ( Figure 1 ) thì bề mặt tọa độ có dạng hình trụ đối xứng quanh trục và đặc trưng cho vùng Doppler không xác định.
- Nửa mặt phẳng Ox v y v chứa nửa trục dương Oyv và tam giác vận tốc ( Figure 2 ) tương ứng với giá trị pha của độ trượt ξ = 0, nửa mặt phẳng Ox v y v chứa nửa trục âm Oy v ( Figure 2 ) tương ứng với giá trị pha của độ trượt ξ = π.
Xác định giá trị trượt mục tiêu của đạn
Để mô tả hoạt động của phần chiến đấu thường sử dụng hệ tọa độ Bxr-yr-zr, có gốc tọa độ đặt tại vị trí kích nổ của phần chiến đấu. Trục Bxr trùng với trục dọc của đạn và có hướng từ trọng tâm tới mũi của đạn.
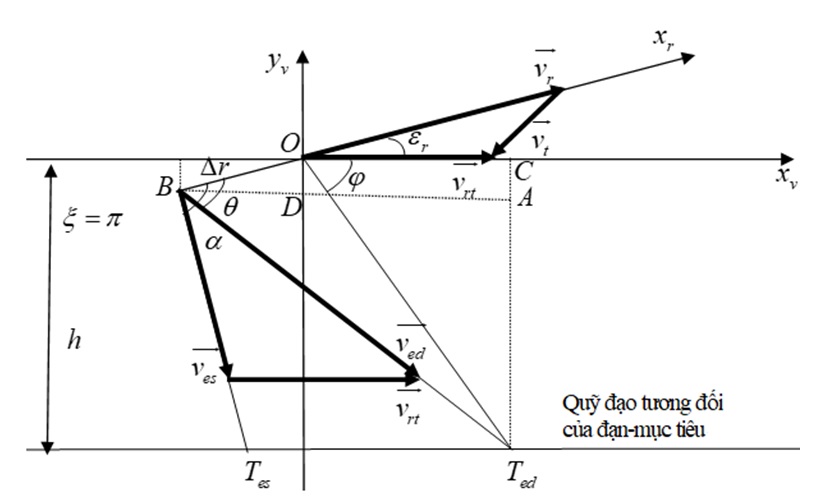
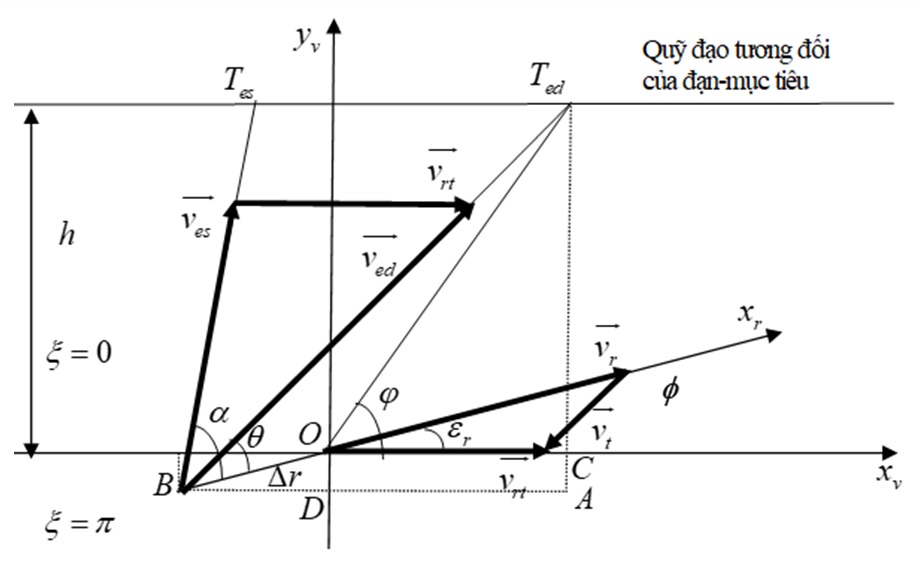
Khi phối hợp sự làm việc của ăng-ten và luồng mảnh thì pha của độ trượt có giá trị: ξ ∈ [0, 2π]. Trong thực tế, đối với phần chiến đấu đối xứng theo trục dọc của đạn và sử dụng ngòi nổ Doppler thì có thể giới hạn giá trị của pha của độ trượt ξ = 0 và ξ = π. Hai trường hợp này được minh họa trên Figure 3 và Figure 4 .
Trong Figure 3 , ε r là góc hướng hợp bởi véc-tơ vận tốc đạn và vận tốc tương đối đạn - mục tiêu; Điểm B là vị trí kích nổ của phần chiến đấu và cách vị trí đặt ăng-ten một khoảng OB = Δr; α là góc bay tán trung bình của mảnh vàng tĩnh; Θ là góc bay tán trung bình của mảnh vàng động; là véc-tơ vận tốc mảnh vàng tĩnh; là véc-tơ vận tốc mảnh vàng động; Tes là giao điểm giữa quỹ đạo mảnh vàng tĩnh và đường thẳng chứa mục tiêu, song song với trục Ox; T ed là giao điểm giữa đường thẳng chứa mục tiêu, song song với trục Ox và hướng chuyển động của mảnh vàng động; φ là góc được tạo bởi trục Oxv và đường thẳng OT ed . Đây là góc mà tại đó hệ thống ra-đa gần đưa ra quyết định kích nổ đạn và được gọi là góc kích nổ đạn. Nó được tạo bởi trục Ox và đường thẳng OT ed ;
Đối với mỗi giá trị trượt h ( Figure 3 ) sẽ ứng với một khoảng giá trị góc kích nổ đạn trong hệ tọa độ vận tốc có gốc tọa độ O và lệnh kích nổ đạn tại thời điểm mảnh vàng và mục tiêu gặp nhau tại điểm T ed .
Công thức tính vận tốc mảnh văng động:
Xét véc-tơ , thời gian để mảnh văng tĩnh đi hết quãng đường BT với vận tốc v es ≠ 0 là:
trong đó: . Mục tiêu sẽ bị tổn thương nếu mảnh văng động và mục tiêu gặp nhau tại vị trí T ed . Khi đó, khoảng cách T es T ed được xác định theo công thức:
trong đó: x vTed > x vTes . Như vậy, véc-tơ vận tốc mảnh vàng động (v ed ≠ 0) hướng vào điểm T ed , thời gian mảnh vàng động đi hết quãng đường BT ed = red được xác định theo công thức:
trong đó: .
Xét trường hợp ξ = π ( Figure 3 ) Trong tam giác vuông ABT ed vuông tại A ta có: ÂBT ed = θ − εᵣ ≠ 0 , suy ra θ ≠ ε r
Trong tam giác vuông BOD vuông tại D ta có OBD = ε r :
OD = CA = OB sin(ÔBD) = OB sin ε r = Δr sin ε r , (6)
AT ed = CT ed − CA = h − Δr sinε r , khi ξ = π
Thay (6) vào (5) ta có:
- Xét trường hợp ξ = 0 ( Figure 4 )
Trong tam giác vuông ABT ed vuông tại A ta có: ÂBT ed = 0, suy ra θ ≠ ε r .
Trong tam giác vuông BOD vuông tại D ta có: ÔBD = ε r
Thay (9) vào (8) ta có:
Theo Figure 3 , Figure 4 , giá trị trượt mục tiêu được xác định bằng công thức:
Thay (7) vào (12) ta có:
Thay (13) vào (11) ta có:
Suy ra,
Thay (10) vào (12) ta có:
Thay (15) vào (11) ta có:
Như vậy, công thức (14) và (16) xác định h tương ứng với pha trượt ξ = π và ξ = 0.
Kết quả, thảo luận
Đánh giá giá trị trượt mục tiêu của đạn phụ thuộc vào một số tham số như góc kích nổ đạn và pha của độ trượt thông qua một số ví dụ sau:
Ví dụ 1: θ = 30 o ; ε r = 15 o ; φ = [0 o , 60 o ]; Δr = 0.3m; ξ = π và ξ = 0. Áp dụng công thức (14) và (16) để xác định giá trị trượt mục tiêu của đạn. Tính toán các giá trị bằng phần mềm Matlab ( Figure 5 ).
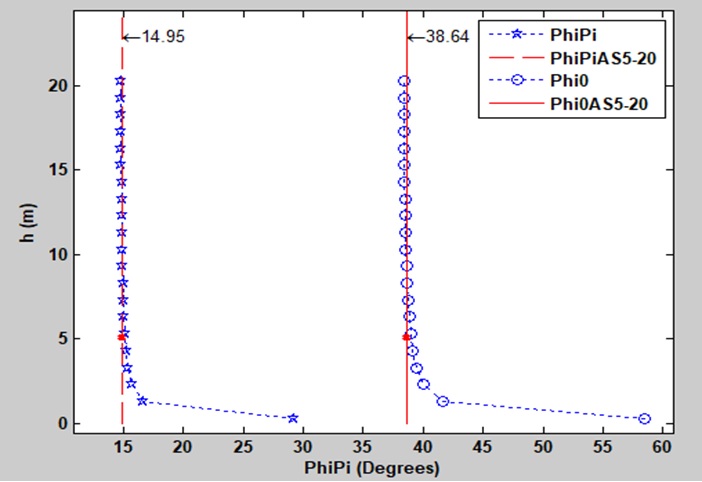
Figure 5 . Giá trị trượt mục tiêu của đạn phụ thuộc vào góc kích nổ đối với pha của độ trượt ξ = π và ξ = 0.
Từ Figure 3 , Figure 4 , Figure 5 , công thức (14) và (16) ta nhận thấy rằng, tại vị trí B ( Figure 3 , Figure 4 ) góc kích nổ φ lớn nhất, khi h tăng dần từ Δrsinε r thì giá trị góc φ giảm dần và thay đổi nhỏ xung quanh giá trị tiệm cận ứng với giá trị độ trượt trong khoảng từ 5m đến 20m. Theo kết quả khảo sát ở Figure 5 , đường tiệm cận PhiPiAS5-20 được máy tính tự động đưa ra thể hiện giá trị góc kích nổ đầu đạn đạt giá trị không đổi là 14.95 o khi giá trị độ trượt bắt đầu từ 5m đến 20m với pha của độ trượt ξ = π và giá trị này là 38.64 o ứng với đường tiệm cận Phi0AS5-20 được máy tính tự động đưa ra thể hiện giá trị góc kích nổ đầu đạn đạt giá trị không đổi khi giá trị độ trượt dao động từ 5m đến 20m và pha của độ trượt ξ = 0. Góc kích nổ cho phép nằm trong khoảng [14.95 o , 27.86 o ] đối với ξ = π và [38.64 o , 58.29 o ] đối với ξ = 0, khi đó độ trượt sẽ có giá trị nhỏ hơn 5m.
Ví dụ 2: θ = 30 o ; ε r = 15 o ; φ = [10 o , 40 o ]; Δr = 0m; ξ = π và ξ = 0. Kết quả tính toán h bằng công thức (14) và (16) trong phần mềm Matlab được thể hiện trên Figure 6 . Khác với ví dụ 1 ở chỗ Δr = 0m, nghĩa là vị trí đặt ăng-ten trùng với vị trí kích nổ đầu đạn.
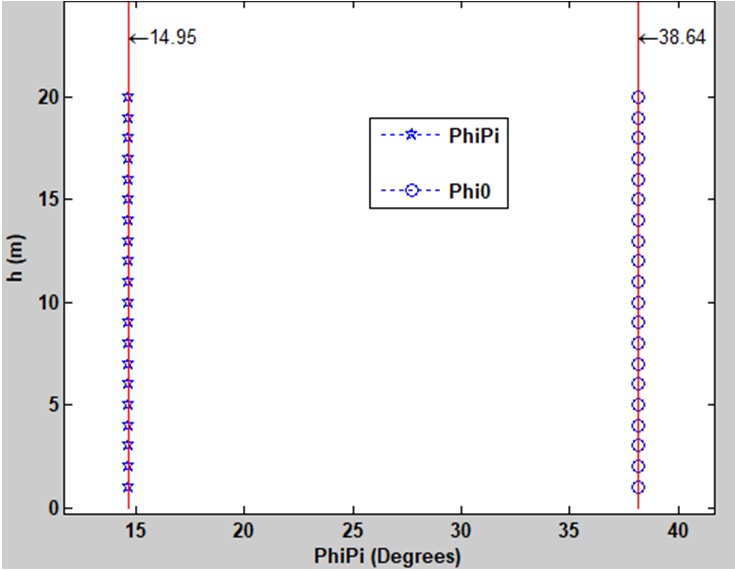
Figure 6 . Giá trị trượt mục tiêu của đạn khi góc kích nổ đạn có giá trị nhỏ nhất.
Theo kết quả nhận được tại Figure 6 , khi Δr = 0m, đối với mọi giá trị trượt h ≤ 20m luôn tồn tại duy nhất một giá trị góc kích nổ 14.95 o tương ứng với giá trị pha trượt ξ = π và giá trị góc kích nổ 38.64 o tương ứng với giá trị pha trượt ξ = 0. Với giá trị Δr = 0m trên thực tế rất khó có thể xảy ra, do cùng với ăng-ten là hệ thống xử lý tín hiệu thu phát phức tạp, chúng có kích thước đáng kể. Vì thế, tùy vào từng loại đạn cụ thể mà có giá trị Δr tương ứng.
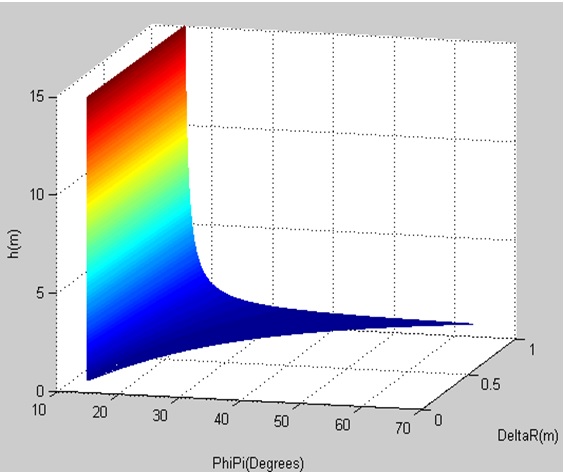
Ví dụ 3: θ = 30 o ; ε r = 15 o ; φ = [0 o , 70 o ]; Δr = [0, 1] m; ξ = π. Tính toán h bằng công thức (14) và (16) trong phần mềm Matlab ( Figure 7 ). Ở đây đánh giá sự thay đổi giữa độ trượt và góc kích nổ khi thay đổi Δr nhằm xác định giá trị trượt tương ứng với từng giá trị góc kích nổ và khoảng cách tương đổi giữa vị trí đặt ăng-ten và điểm kích nổ.
Theo kết quả được thể hiện trên Figure 7 ta thấy rằng, giá trị Δr tỷ lệ thuận với độ rộng khoảng giá trị góc kích nổ khi độ trượt nhỏ hơn 5m. Cụ thể đối với trường hợp pha của độ trượt ξ = π khi Δr = 0m thì góc kích nổ đạn là 14.95 o đối với mọi giá trị độ trượt và khi Δr = 1m thì góc kích nổ sẽ nằm trong khoảng (14.95 o , 62.874 o ] với giá trị độ trượt trong khoảng (0, 5] m. Khi độ trượt lớn hơn 5m, thì góc kích nổ có giá trị gần đúng bằng φ = φ min = 14.95 o = const đối với mọi giá trị Δr. Trong trường hợp này, để kiểm soát được độ trượt h thì góc kích nổ phải có giá trị trong khoảng (14.95 o , 62.874 o ] và Δr = (0, 1] m.
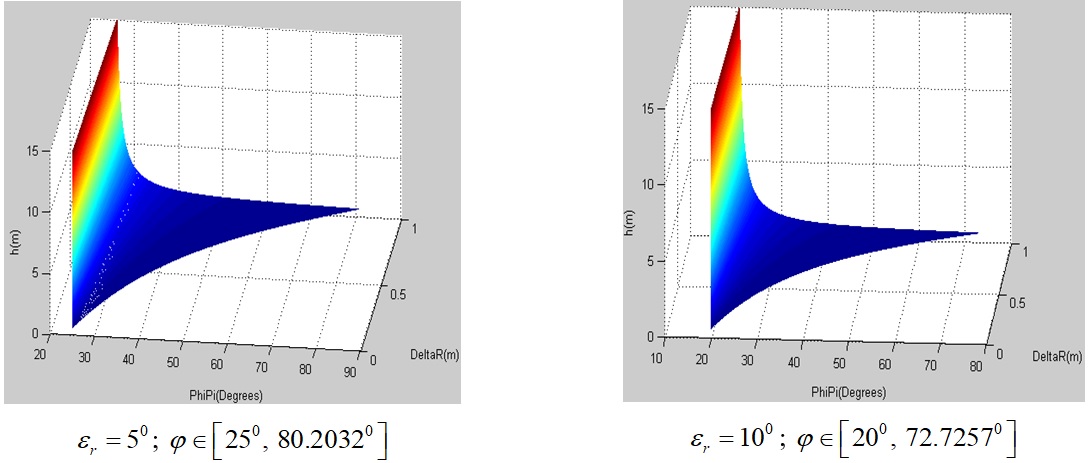
Ví dụ 4: θ = 30 o ; ε r = 5 o ; h = (0, 15] m và ε r = 10 o ; Δr = [0, 1] m; ξ = π. Kết quả tính toán h bằng (14) và (16) trong phần mềm Matlab được thể hiện trên Figure 8 . Ở trường hợp này khảo sát sự thay đổi h đối với 2 trường hợp góc hướng lần lượt là ε r = 5 o và ε r = 10 o để xác định giá trị ε r .
Kết quả chỉ ra giá trị trượt h đạt giá trị lớn nhất khi φ đạt giá trị nhỏ nhất, và ngược lại khi φ tăng thì h giảm. Khi góc hợp bởi véc-tơ vận tốc đạn và vận tốc tương đối đạn-mục tiêu (ε r ) tăng, góc kích nổ (φ) giảm.
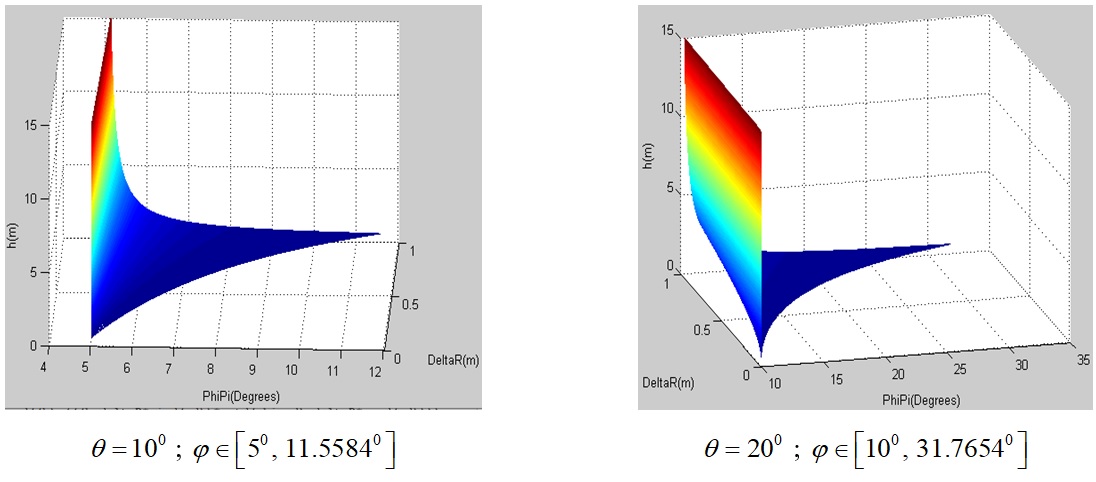
Ví dụ 5: ε r = 15 o ; θ = 10 o ; θ = 20 o ; Δr = [0, 1] m; ξ = π. Tính h bằng (14) và (16) trong phần mềm Matlab ( Figure 9 ). Ví dụ này khảo sát sự thay đổi giá trị trượt mục tiêu đối với 2 trường hợp của góc bay tản của mảnh văng động lần lượt là θ = 10 o và θ = 20 o với mục đích xác định giá trị θ có ảnh hưởng như thế nào đến giá trị h hay.
Khi góc bay tản của mảnh văng động (θ) tăng thì giá trị góc kích nổ (φ) tăng. Điều đó có nghĩa là góc kích nổ đạn phụ thuộc vào vận tốc của đạn. Giá trị θ ảnh hưởng không đáng kể đến giá trị h.
Kết luận
Giải phương trình (14) và (16) cho phép xác định giá trị trượt mục tiêu của đạn đối với các tham số kết cấu cụ thể. Với những lý giải, phân tích ở trên kết quả thu được là cơ sở xác định các thông số khác trong ngòi nổ không tiếp xúc của đạn như góc kích nổ φ, pha độ trượt ξ, khoảng cách giữa ăng-ten và vị trí kích nổ Δr, góc bay tản trung bình của mảnh văng động θ, và đó cũng là công việc phải tiến hành khi thiết kế ngòi đạn. Việc xây dựng các tham số và phương pháp giải sẽ được tác giả trình bày vào dịp khác. Kết quả thu được mở ra một số hướng như kích nổ đa điểm, thiết kế ăng-ten nhỏ gọn để đảm bảo lắp được nhiều trên các loại đạn, đánh giá sự sống sót của mục tiêu sau khi trúng mảnh văng...
Xung đột lợi ích
Tác giả xin cam đoan không có bất kì xung đột lợi ích nào trong công bố bài báo.
Đóng góp tác giả
Phạm Xuân Quyền tác giả duy nhất thực hiện toàn bộ bản thảo.
References
- Huang ZH, Feng QJ. Research on optimum fuze-warhead coordination based on antenna beamforming of fuze. In: The 2007 International Autumn Seminar on Propellants, Explosives and Pyrotechnics; 2007 Oct 23–26; Xi'an, China. p. 861–4. . ;:. Google Scholar
- Zhao Q, Du GY, Zhang B, et al. Simulation design of fuze warhead system of air defense missile at very low altitude. J Syst Eng Electron. 2017;28(3):572–84. . ;:. Google Scholar
- Veksin S. Processing of radar signals in Doppler homing heads. Moscow: MAI; 2005. 304 p. . ;:. Google Scholar
- Kolodny MA. Radar proximity fuzing and the Cold War paradigm. In: Microwave Symposium Digest (MTT), 2011 IEEE MTT-S International; 2011. . ;:. Google Scholar
- Li ZB. Implementation and development of compact UWB proximity fuze sensor system. In: Computational Problem-Solving (ICCP), 2011 International Conference; 2011. . ;:. Google Scholar
- Astapov YM, Kozlov VI, Soboleva NS, Khokhlov VK, Borzov AB, Avtonomnye ED. Autonomous information and control systems. In: Proc. of Department of Autonomous Information and Control Systems of Bauman MSTU. Vol. 1. 2011. p. 409–64. . ;:. Google Scholar
- Klement C, Comanescu IS, Clinciu M. The mathematical model of the simulation of the Doppler effect. In: ICMS 2019 & COMEC 2019; Brasov, Romania. 2019;5(1):105. . ;:. Google Scholar
- Phạm XQ. Xác định sự phụ thuộc của tần số doppler vào độ trượt giữa đạn pháo và mục tiêu khi sử dụng ngòi nổ không tiếp xúc Dopler. Tạp chí Khoa học Tự nhiên - Kỹ thuật - Công nghệ, Đại học Thái Nguyên. 2023;228(2). . ;:. Google Scholar

 Open Access
Open Access